LES CLES DU DIMENSIONNEMENT
Ouvrages en commandePhotovoltaïque autonome
Photovoltaïque raccordé au réseau

Formations Professionnelles Photovoltaïques
Principe de production du froid > Cycle frigorifique ditherme
Pour mettre en oeuvre un cycle frigorifique, il est donc nécessaire de disposer d’au moins deux sources de chaleur (figure 1.2. L’une sera appelée source froide (celle dont on va extraire la chaleur) et l’autre la source chaude (celle où l’on va rejeter la chaleur). Appliquons le premier principe à un cycle décrit entre ces deux sources :
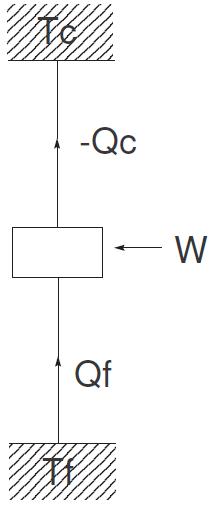
FIGURE 1.2 – Cycle ditherme
Qf + Qc + W = 0 (1.3)
où Qf est la chaleur reçue de la source froide, Qc la chaleur reçue de la source chaude et W l’énergie mécanique reçue. Le second principe nous permet d’écrire, pour un cycle réversible et en supposant que les échanges de chaleur se font à la température des sources :
Qf / Tf + Qc / Tc = 0 (1.4)
d’où :
Qc = -Qf × Tc / Tf (1.5)
Si on reporte cette expression dans l’équation 1.3, on obtient :
W = Qf × (Tc / Tf -1) (1.5)
La température Tc de la source chaude étant supérieure à la température de la source froide Tf , et si la chaleur Qf est positive (on souhaite refroidir, donc extraire de la chaleur de la source froide), le travail reçu W est donc positif.
Il faut donc ainsi nécessairement apporter un travail mécanique lors d’un cycle ditherme pour obtenir un effet frigorifique.
Coefficient de performance
Le coefficient de performance d’un cycle frigorifique, noté COP se définit comme le rapport entre ce que l’on récupère (la chaleur extraite de la source froide) par rapport à ce que l’on apporte (l’énergie mécanique). On a ainsi :
COP = Qf / W (1.7)
Dans le cas du cycle ditherme, en reprenant l’expression 1.6, on obtient l’expression du coefficient de performance dans le cas d’un cycle réversible :
COP = 1 / (Tc / Tf - 1) (1.8)
d’où l’expression de l’efficacité maximum pouvant être atteinte par un cycle ditherme (efficacité de Carnot) :
COP = Tf / (Tc - Tf) (1.9)
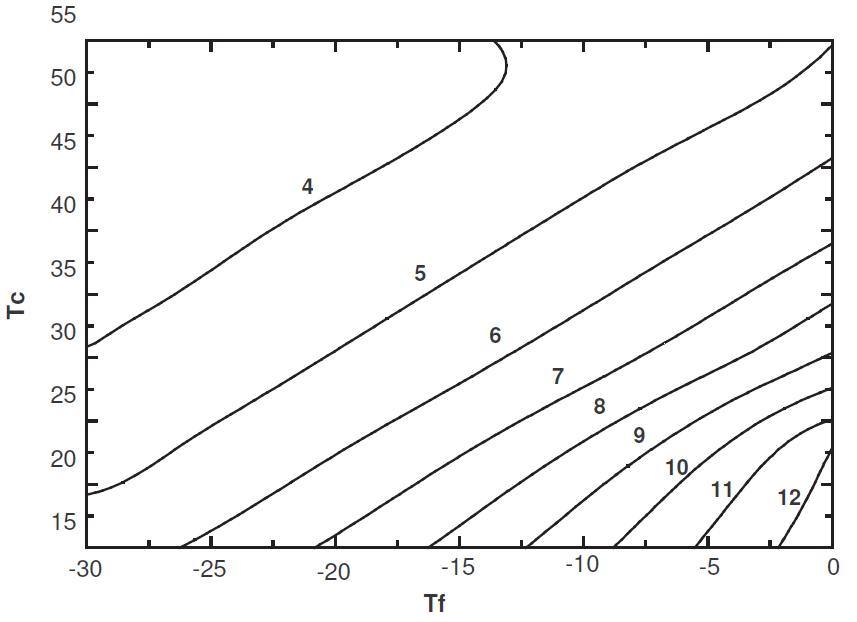
FIGURE 1.3 – Efficacité de Carnot en fonction des températures des sources
Cycle de Carnot
Sadi Carnot a posé en 1824 dans son ouvrage "Réflexions sur la puissance motrice du feu et les machines propres à développer cette puissance" les bases d’un cycle idéal entre deux sources de chaleur, connu depuis sous le nom de "cycle de Carnot". Celui-ci est composé de deux isentropes adiabatiques et de deux isothermes. Un exemple (cycle moteur) est donné dans la figure 1.4 et l’efficacité de ce cycle est donnée par la formule 1.9.
Si l’on fait fonctionner ce cycle en sens opposé, on obtient un cycle qui absorbe de la chaleur à la source froide et qui en dégage à la source chaude. Il s’agit donc bien d’un cycle frigorifique, on parle alors communément de "cycle inverse".
Les cycles réels à compression de vapeur, tels que celui présenté dans la figure 1.8 diffèrent principalement du cycle présenté dans la figure 1.4 en deux points :
- on effectue la compression d’un gaz, et non d’un mélange diphasique
- le gaz est détendu sans récupération d’énergie mécanique, cette détente n’est donc pas isentropique
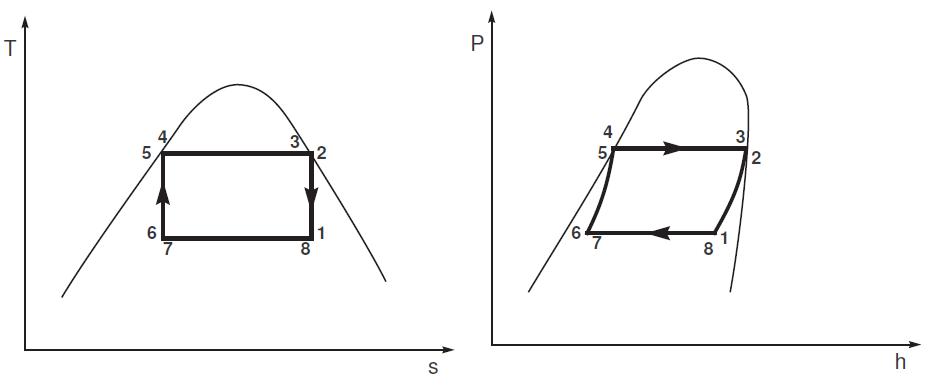
FIGURE 1.4 – Exemple d’un cycle moteur de Carnot : représentation P-h et T-s
Ainsi, pour des raisons technologiques, la détente n’étant pas isentropique et l’échange de chaleur avec la source chaude non isotherme, l’efficacité du cycle réel à compression de vapeur est par conception inférieure à l’efficacité du cycle de Carnot.
Phénomènes endothermiques
Le cycle le plus utilisé actuellement pour "produire du froid" est le cycle à compression de vapeur. Ce cycle utilise un phénomène endothermique spécifique : la vaporisation d’un liquide. Cependant, de nombreux phénomènes endothermiques existent et plusieurs peuvent ou sont utilisés pour obtenir un effet frigorifique (tableau 1.1).
La vaporisation d’un fluide est utilisée dans le cycle à compression de vapeur, mais est également souvent utilisée dans des systèmes ouverts (refroidissement par cryogénie, par azote liquide par exemple) : le fluide n’est alors pas récupéré, mais perdu.
La fusion d’un solide est principalement utilisée pour stocker le froid ou pour le transporter plus efficacement : frigoporteurs diphasiques, stockage du froid par des matériaux à changement de phase.
La désorption d’un gaz d’un solide est utilisée dans le cycle à adsorption et la désorption d’un gaz d’un liquide dans le cycle à absorption. Ces cycles mettent en oeuvre 3 sources de chaleur.
| Phénomènes | Commentaires |
|---|---|
| Vaporisation d’un liquide | Ex : vaporisation d’azote liquide (pour l’eau, à P=1 atm, Lv = 2258 kJ/kg ) |
| Fusion d’un solide | Ex : glaçon dans le pastis ! (pour la glace Lf = 333 kJ/kg ) |
| Sublimation d’un solide | Ex : glace carbonique |
| Désorption d’un gaz d’un liquide ou d’un solide | Ex : cycle à absorption et adsorption |
| Détente d’un gaz dans certaines conditions | Ex : détente d’air |
| Effet Peltier | Echauffement de jonctions de métaux alimentés electriquement |
| Dissolution d’un soluté dans un solvant | |
| Désaimantation d’un métal paramagnétique | Effet frigorifique pour quelques métaux rares |
| TABLE 1.1 – Phénomènes endothermiques | |
Il existe des modules de refroidissement utilisant l’effet thermoélectrique Peltier. Ces unités sont notamment utiles lorsque la mise en oeuvre d’une machine frigorifique utilisant un liquide pose des problèmes pratiques ou de sécurité (refroidissement de composants électroniques par exemple). Le rendement de ces modules est faible et dégage donc beaucoup plus de chaleur qu’il n’en extrait du corps à refroidir, chaleur qu’il faut évacuer. Enfin l’effet paramagnétique est l’objet de nombreuses recherches actuellement. Des prototypes de réfrigérateur de faible puissance utilisant cette technologie ont été developpés récemment dans plusieurs laboratoires.
Cycle à compression sans changement de phase
On oublie souvent que le cycle à compression de vapeur peut être effectué sans changement de phase. C’est le cas par exemple du cycle à air fermé, tel que décrit dans le diagramme de la figure 1.5.
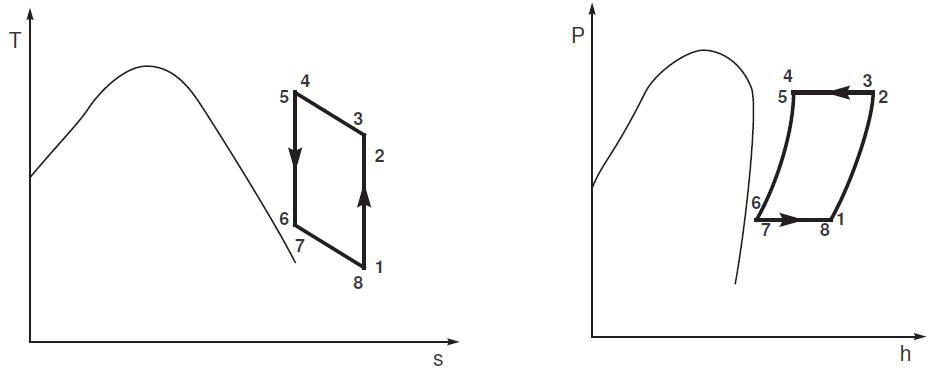
FIGURE 1.5 – Exemple d’un cycle à air fermé : représentation P-h et T-s
Ce cycle est ainsi constitué de quatre composants :
- un système de compression
- deux échangeurs de chaleur
- un système de détente
L’énergie nécessaire pour compresser l’air d’un état 1 à un état 2, si on suppose que son comportement est celui d’un gaz parfait, est :
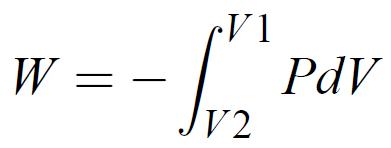 (1.10)
(1.10)
La compression étant supposée adiabatique, on a :
PVγ = CONSTANTE (1.11)
L’équation 1.10 peut donc s’écrire :
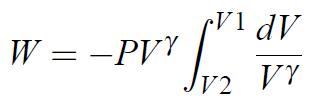 (1.12)
(1.12)
En intégrant cette équation, on obtient :
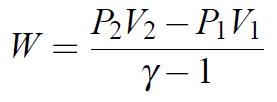 (1.13)
(1.13)
L’air étant considéré comme un gaz parfait, dont le comportement est régi par l’équation PV = nRT, on peut écrire :
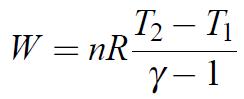 (1.14)
(1.14)
Le coefficient de performance d’un cycle tel que présenté dans la figure 1.5 peut ainsi être exprimé par :
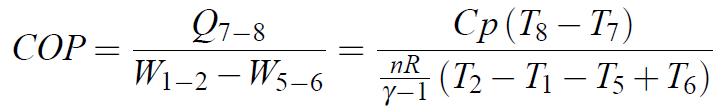 (1.15)
(1.15)
Puisque Cp = n×R / (1-1/γ), on obtient l’expression :
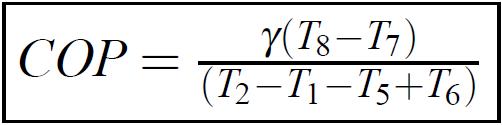 (1.16)
(1.16)
Une application numérique est présentée dans la figure 1.6 :
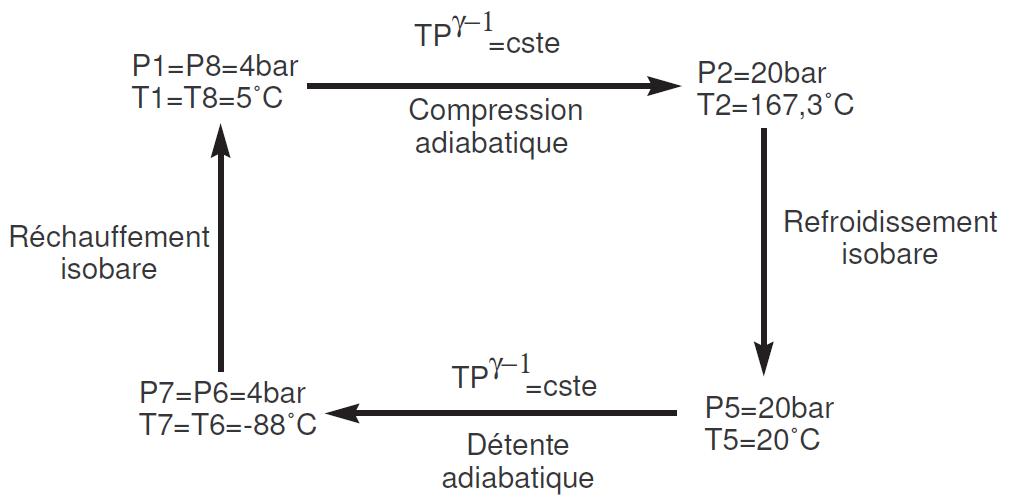
FIGURE 1.6 – Application numérique cycle à air
La valeur du coefficient de performance pour cet exemple, où l’on échange avec une source froide à 5°C et une source chaude à 20°C est (avec &gamma=1,4):
COP = 2,4 (1.17)
Même en négligeant ici les irréversibilités de la compression et de la détente, cette efficacité est néanmoins plus faible que celle que nous pourrions obtenir avec un cycle à compression de vapeur avec changement de phase, telle que présenté dans le paragraphe suivant.
Cycle à compression de vapeur avec changement de phase
Ce cycle à compression de vapeur est constitué d’au moins quatre composants :
- un système de compression
- deux échangeurs de chaleur
- un système de détente
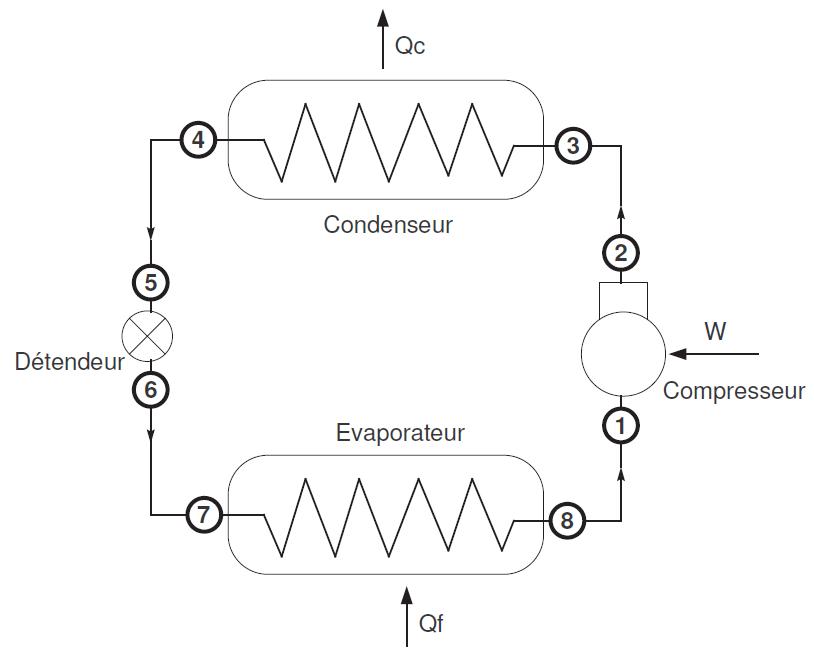
FIGURE 1.7 – Système frigorifique à compression mécanique de vapeur
Ce système est composé de :
- Un évaporateur : le frigorigène se vaporise dans cet échangeur. La vapeur sortante peut être saturante ou le plus souvent légèrement surchauffée. L’évaporation est effectuée à pression constante (si l’on néglige les pertes de pression dans l’échangeur), et donc à temperature constante pour les fluides purs
- Un compresseur : il aspire la vapeur surchauffée sortant de l’évaporateur, et la comprime jusqu’à la pression qui règne dans le condenseur, et la rejette dans celui-ci
- Un condenseur : le frigorigène se condense dans cet échangeur. Le liquide sortant est à saturation ou légèrement sous refroidi
- Un détendeur : il alimente l’évaporateur avec un fluide à basse pression. Le fluide y subit une détente de la pression de condensation à la pression d’évaporation
Le tracé de ce cycle, appelé cycle Evans-Perkins, sur les diagrammes T-s et P-h est présenté dans la figure 1.8. Sur ces diagrammes, le fluide subit la série transformations suivantes :
- Compression isentropique de 1 à 2
- Refroidissement des vapeurs surchauffées de 3 à 3’ (isobare)
- Condensation isotherme de 3’ à 4
- Détente isenthalpique de 5 à 6
- Evaporation isotherme de 7 à 8
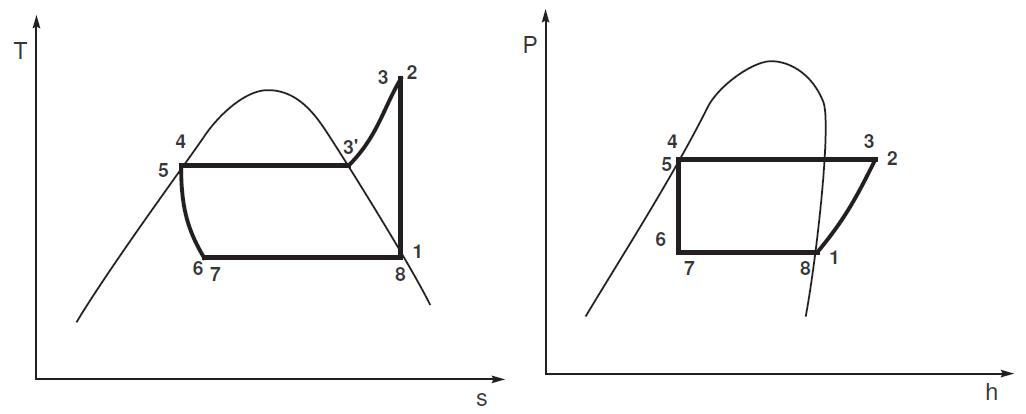
FIGURE 1.8 – Tracés du cycle de réfrigération à compression de vapeur dans les diagrammes T-s et P-h
Exemple et application numérique
Reprenons le cas présenté pour le cycle à air avec une source chaude à 20°C et une source froide à 5°C.
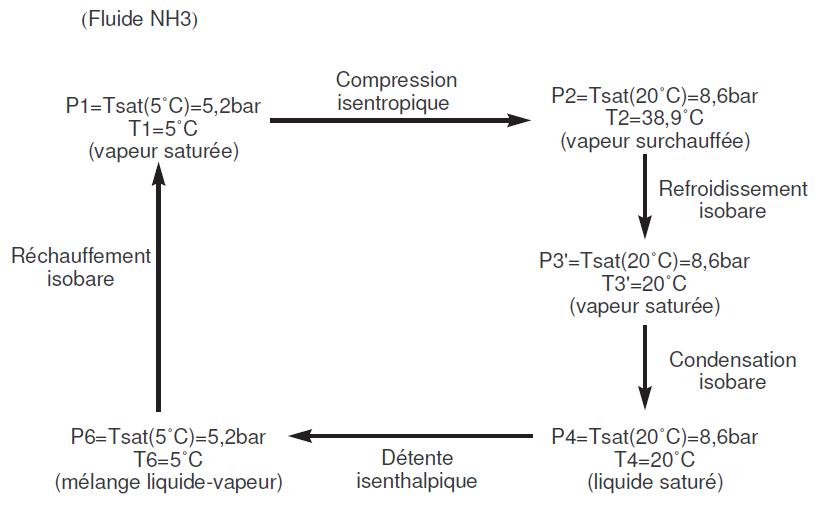
FIGURE 1.9 – Application numérique cycle à compression de vapeur avec changement de phase
Le coefficient de performance du cycle Evans Perkins, en négligeant les irréversibilités de la compression et en supposant que l’évaporation et la condensation s’effectuent à la température des sources est :
COP = (h8 - h7) / (h2 - h1) (1.18)
où h est l’enthalpie du fluide.
où h est l’enthalpie du fluide.
Dans le cas de l’ammoniac, on obtient h8 - h7 = 1173 kJ/kg et h2 - h1 = 67,4 kJ/kg, soit un COP de 17,4, à comparer au COP obtenu pour le cycle à air (2,4). L’efficacité de Carnot pour ce cycle est :
COPCarnot = Tf / (Tc - Tf) = 278 / 15 = 18,5 (1.19)
Conséquence des écarts de température entre le fluide et les températures des sources
L’évaporation et la condensation dans un cycle Evans Perkins ne peut s’effectuer exactement à la température des sources. En effet, les résistances thermiques des échangeurs imposent des écarts de température entre les sources et le fluide. Ceci peut être exprimé par :
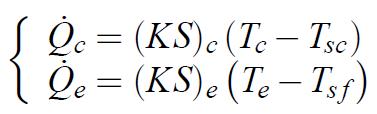 (1.20)
(1.20)où Qc est la puissance échangée au condenseur, KS est la conductance thermique globale de l’échangeur, Tc la température de condensation et Tsc la température de la source chaude, Qe est la puissance échangée à l’évaporateur, Te la températured’évaporation et Tsf la température de la source froide.
L’application du premier et du second principe permet d’écrire :
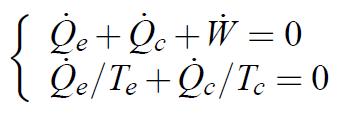 (1.21)
(1.21)
En combinant les équations précédentes, le coefficient de performance peut être exprimé par :
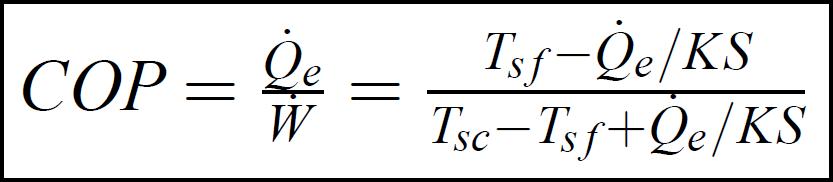 (1.22)
(1.22)
où KS est défini par :
1 / KS = 1 / (KS)c + 1 / (KS)e (1.23)
Si l’on trace le coefficient de performance en fonction de la puissance frigorifique, on obtient une fonction monotone décroissante. Ainsi la performance d’une machine frigorifique à compression de vapeur tendra à diminuer lorsque l’on la fera fonctionner à pleine charge plutôt qu’à charge partielle.
La performance peut par contre être améliorée en augmentant la qualité des échangeurs (le paramètre KS), par exemple en augmentant les surfaces d’échange, ou en améliorant la qualité de l’échange thermique.
Application numérique
Reprenons l’exemple précédent avec une température de source chaude à 20 °C et une température de source froide à 5 °C. On supposera que KSc = 2 kW/K et KSe = 2 kW/K, soit KS = 1kW/K. Pour une puissance de 20 kW (soit un écart de 10 °C entre la température d’évaporation et la température de la source froide), la valeur du coefficient de performance est de 7,4 , à comparer à la valeur de 17,4 trouvée dans le paragraphe précédent.
Pour une puissance de 10 kW, la valeur du coefficient de performance est de 10,7.