LES CLES DU DIMENSIONNEMENT
Ouvrages en commandePhotovoltaïque autonome
Photovoltaïque raccordé au réseau

Formations Professionnelles Photovoltaïques
Efficacité du cycle à compression de vapeur
Le cycle à compression de vapeur est le cycle le plus utilisé pour les machines frigorifiques, principalement pour des raisons de performance. Comme on l’a vu dans les paragraphes précédents, l’efficacité de Carnot peut être vu comme une référence de performance maximale, même si la nature du cycle à compression de vapeur fait que cette performance ne peut être jamais atteinte
Notion d’exergie
Les irréversibilités réduisent également la performance des cycles frigorifiques réels. Celles-ci peuvent être analysées, soit par un bilan de production d’entropie, soit par un bilan de destruction d’exergie. Les deux diffèrent principalement sur la manière de traiter le problème car elles sont toutes deux basées sur l’application du premier et second principe. La destruction d’exergie a cependant l’avantage d’être un peu plus intuitive : il est plus logique de parler de "destruction" de quelque chose si l’on a des irréversibilités que de "production".
Pour illustrer ceci, prenons le cas d’un cycle moteur, par exemple une machine à vapeur, entre une source chaude à la température Tc et la température ambiante T0. Si l’on applique le premier et le second principe pour un cycle ditherme irréversible, on a :
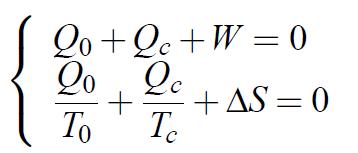 (1.31)
(1.31)ΔS est l’entropie produite au cours du cycle.
A partir des équations précédentes, on peut exprimer l’énergie mécanique produite :
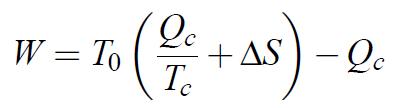 (1.32)
(1.32)
qui peut réécrite sous la forme :
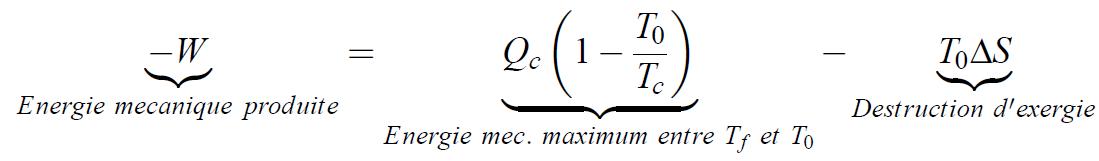 (1.33)
(1.33)
Le terme gauche de l’équation 1.33 représente l’énergie mécanique produite au cours du cycle. On reconnait dans le terme Qc×(1-T0 / Tc) l’énergie mécanique maximum que pourrait produire un cycle moteur réversible entre T0 et Tc (on parle de flux d’exergie entrant). C’est la "valeur" en terme d’énergie mécanique que représente une source de chaleur à la température Tc. Enfin le terme T0ΔS représente en quelque sorte la pénalité en terme d’énergie mécanique due aux irréversibilités . Il s’agit de la destruction d’exergie.
Le rendement exergétique est dans ce cas du cycle moteur :
 (1.34)
(1.34)
Dans le cas d’un cycle de machine frigorifique effectué entre une source froide à la température Tf et la température ambiante T0, on apporte de l’exergie pure sous forme de travail mécanique W.
Le rendement exergétique peut être exprimé sous la forme :
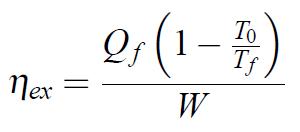 (1.35)
(1.35)
On reconnaît dans cette expression celle du coefficient de performance frigorifique Qf / W et celle du coefficient de performance du cycle de Carnot 1 - T0 / Tc. On peut donc réécrire l’expression du rendement exergétique d’un cycle frigorifique ditherme sous la forme :
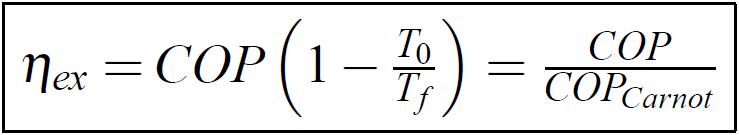 (1.36)
(1.36)
Ce rendement exergétique est une valeur comprise entre 0 et 1 et représente la "qualité" thermodynamique du cycle thermodynamique.
Diagramme T-s et destructions d’énergie
Le diagramme T-s permet de représenter graphiquement les destructions d’exergie tout au long du cycle et en particulier au niveau de chaque composant. Rappelons que l’enthalpie échangée pour une transformation isobare entre un état 1 et un état 2 est :
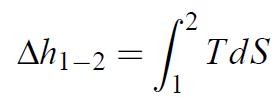 (1.37)
(1.37)
et peut se représenter sur le diagramme T-s par l’aire entre l’axe des abscisses et le chemin décrit entre 1 et 2, comme illustré dans la figure 1.13 :
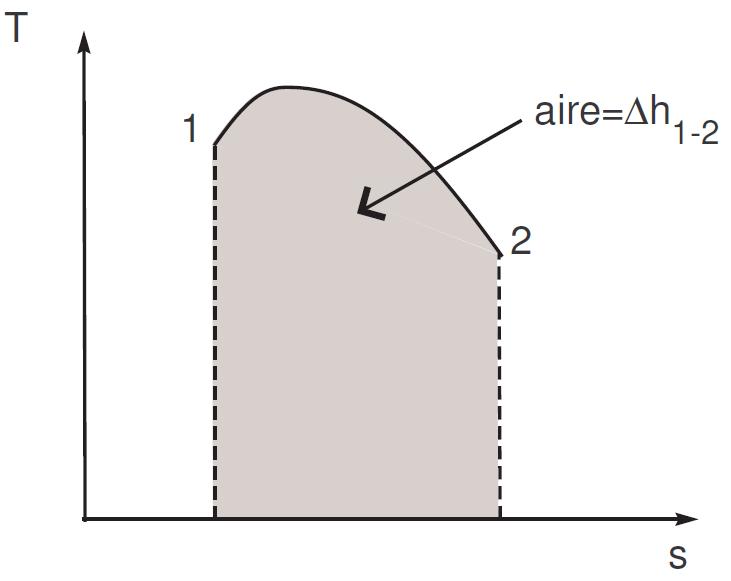
FIGURE 1.13 – Représentation de la variation d’enthalpie dans le diagramme T-s
Destruction d’exergie du cycle Evans-Perkins
Si l’on représente un cycle à compression de vapeur et le cycle réversible entre l’ambiance à la température T0 et une source froide à la température Tf , on obtient le diagramme présenté dans la figure 1.14.
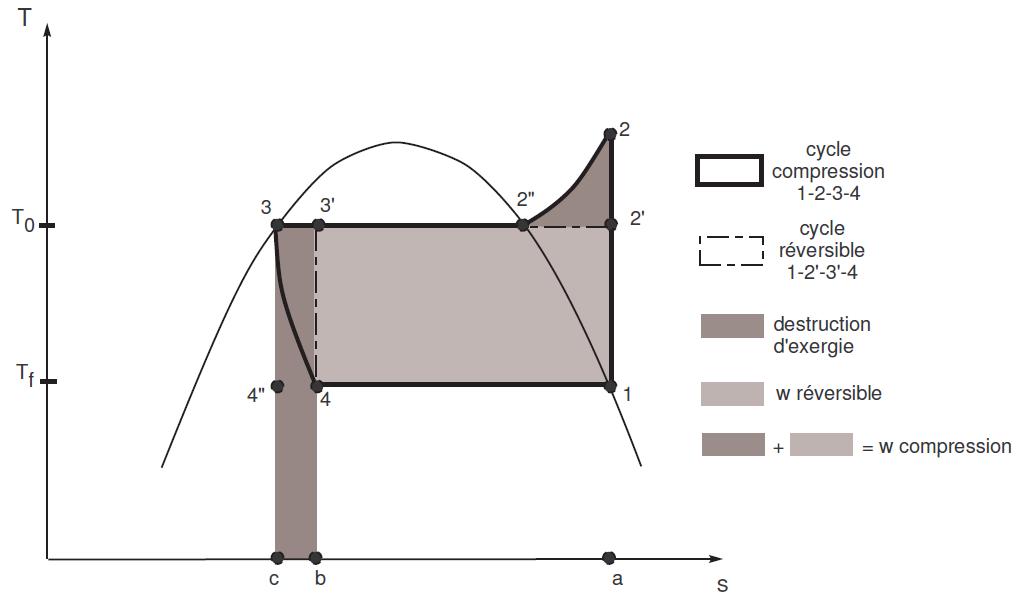
FIGURE 1.14 – Représentation du cycle à compression de vapeur dans le diagramme T-s
L’énergie frigorifique Qf = Δh4-1 est représentée par l’aire a-1-4-b. La chaleur Q0 libérée par le condenseur pour le cycle à compression de vapeur est l’aire a-2-3-c. Le travail de compression est telle que W = Qc-Qe et donc représentée par l’aire 1-2-3-c-b-4-1.
Pour le cycle réversible, le travail de compression est représentée par l’aire 1-2’-3’-4.
La différence entre les deux puissances est due aux irréversibilités, et les aires sont représentatives des destructions d’exergie. En effet, la destruction d’exergie au niveau du condenseur peut être obtenue par le bilan suivant :
Lcond = h2-h3-T0 (s2-s3) (1.38)
ce qui graphiquement peut être représenté par l’aire 2’-2-2". Cette destruction est due au fait que l’échange de chaleur n’est pas isotherme, comme c’est le cas pour le cycle réversible.
La destruction d’exergie au niveau du détendeur est :
Ldet = h3-h4-T0 (s3-s4) (1.39)
Rappelons que l’on h3-h4 = 0 car la détente est supposée isenthalpique. La destruction d’exergie peut donc être représentée par l’aire b-3’-3-c.
Ainsi la représentation des destructions d’exergies dans le diagramme T-s permet de visualiser les irréversibilités du cycle Evans-Perkins, et de quantifier leur importance.