Approche conceptuelle du ruissellement > Les modèles de type réservoir > Formulation mathématique et résolution numérique

Un modèle à réservoir peut être caractérisé par le système d'équations suivant :



• Une équation de continuité :
  dV_S(t) / dt = Q_e(t) - Q_s(t)
• Une équation de stockage :
  V_S(t) = f( Q_e(t) ; Q_s(t) )
  
  Avec :

  • V_S(t) : volume stocké à l'instant t (m³)
  • Q_e(t) = A × IMP × i(t) : flux entrant (m³/s), avec A surface du bassin versant (ha), IMP le coefficient d’imperméabilisation (-) et i(t) l’intensité de la pluie (mm/h)
  • Q_s(t) : flux sortant (débit à l'exutoire) (m³/s).

Ces lois générales s'écrivent différemment selon la fonction f qui relie Vs(t) aux flux entrant et sortant. Les 3 modèles les plus connus sont :

• Le modèle général de Muskingum :
  V_S(t) = K × ( α × Q_e(t) + (1-α) × Q_s(t) )
  Avec α ∈ [0;1]


• Le modèle du réservoir linéaire, avec α = 0 :
  V_S(t) = K × Q_s(t)
  Avec α ∈ [0;1]


• Le modèle avec α = 1 :
  V_S(t) = K × Q_e(t)
  Avec α ∈ [0;1]

Les deux derniers modèles sont simplement des cas particuliers du premier.

Le système composé des deux équations de stockage et de conservation se résout soit par intégration directe, soit par discrétisation. Cette deuxième technique est la plus rapide à mettre en oeuvre. On dérive la loi de stockage par rapport au temps t, et on égalise avec les termes de droite de l’équation de conservation :



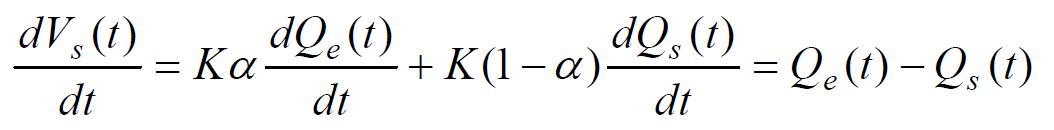
On discrétise directement cette équation différentielle. Pour cela, il existe plusieurs possibilités selon les opérateurs algébriques retenus. Dans tous les cas, on obtient une relation du type :


Les principaux schémas courants de discrétisation et les coefficients C1, C2 et C3 correspondants sont données dans le tableau ci-dessous :

Intégration numérique

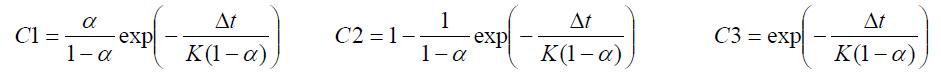
Discrétisation n° 1

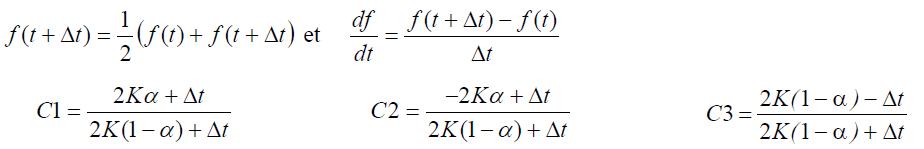
Discrétisation n° 2

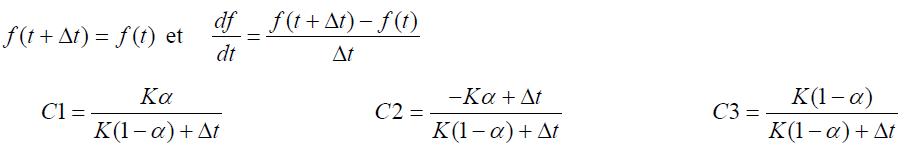
Modèle de Koussis (1976)

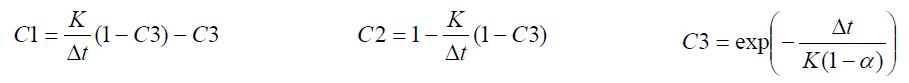
Modèle de Cunge – Cayla (1980)

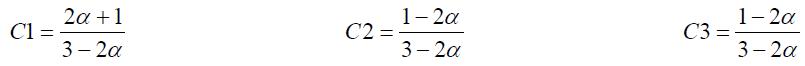
Schémas de discrétisation et coefficients Cj du modèle réservoir linéaire

La résolution par discrétisation présente l'avantage d'une formulation mathématique plus simple. Par contre, elle peut présenter des problèmes de convergence des calculs pour certaines valeurs du triplet (K, a, ?t) qui rendent négatif un des coefficients Cj : il faut donc choisir une valeur de Δt adéquate (Thibault, 1979). Le Tableau 3.2 donne les conditions de positivité des coefficients Cj.

	C1	C2	C3
Intégration numérique	-		-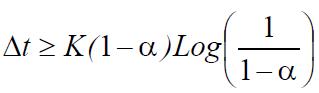
Discrétisation 1	-	Δt ≥ 2 × K × α	Δt ≤ 2 × K × (1-α) (si α = 1 et C3 < 0)
Discrétisation 2	-	Δt ≥ K × α	-
Conditions de stabilité des modèles issus du modèle Muskingum

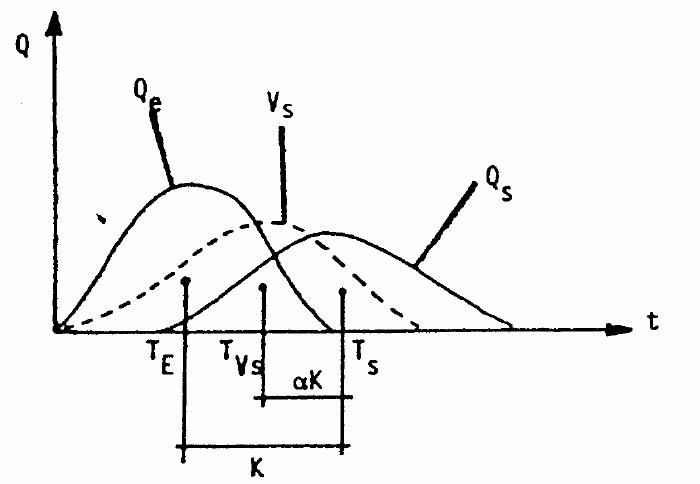
Les calculs ne sont stables que pour a < 0.5. Ces problèmes de convergence disparaissent en utilisant la solution analytique, laquelle permet en outre de déterminer la signification physique des paramètres K et a au moyen d'une transformée de Laplace. On trouve alors que :





Si l'on considère le modèle le plus simple (réservoir linéaire avec α = 0), l'intégration conduit à :



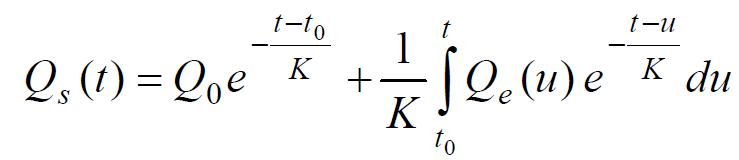
Si on suppose que pour t = 0 on a Q₀ = 0 (débit nul au temps zéro), on se ramène à :



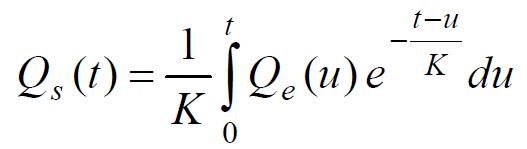
En posant la fonction de Dirac :



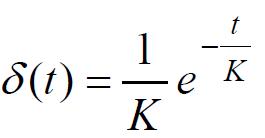
on peut écrire le produit de convolution suivant :